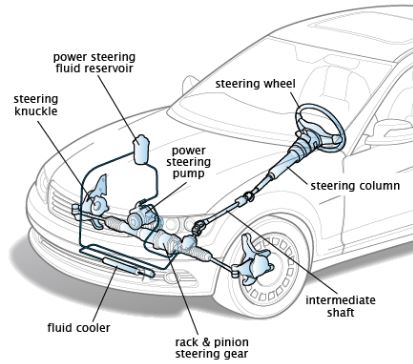
Stress-Strain Problems and solutions:
A wire of length 2.50 m has a per-
centage strain of 0.012% when loaded with a tensile force. Determine the extension of the wire.
Solution:
Original length of wire = 2.50 m = 2500 mm
and strain = 0.012
100 = 0.00012
Strain ε = extension/originallength =x/L,
extension x = εL = (0.00012)(2500) = 0.30 mm
2) (i) A rectangular section metal bar
has a width of 10 mm and can support a maximum
compressive stress of 20 MPa; determine the
minimum breadth of the bar when loaded with a
force of 3 kN.
(ii) If the bar in (a) is 2 m long and
decreases in length by 0.25 mm when the force is
applied, determine the strain and the percentage
strain.
(i) Since stress, σ = force/area
=F/ σ
then, area, A = 6
= 3000 N/20×10^6 Pa
= 150 × 10^–6 m2 = 150 mm2
Cross-sectional area = width × breadth, hence
breadth = area 150
width 10 = = 15 mm
(b) Strain, ε = contraction 0.25
original length 2000 = = 0.000125
Percentage strain = 0.000125 × 100 = 0.0125%
3). A bar 1.60 m long contracts axially
by 0.1 mm when a compressive load is applied to
it. Determine the strain and the percentage strain.
Strain ε = contraction/original length
=0.1mm/1.60×10^3mm
=0.1/1600
=0.000625
Percentage strain = 0.0000625 × 100 = 0.00625%